Физики создали новые факторы понимания гиперболических пространств

В статье, опубликованной на днях в издании Physical Review, группа ученых профессора Коллара и научного сотрудника Алексея Горшкова, физика Национального института стандартов и технологий и научного сотрудника Объединенного центра квантовой информации и компьютерных наук, были представлены абсолютно новые математические инструменты для лучшего понимания моделирования гиперболических пространств.
Исследование основано на предыдущих экспериментах Коллара по моделированию упорядоченных решеток в гиперболическом пространстве с помощью микроволнового света, содержащегося на микросхемах. Их новый набор инструментов включает то, что они называют «словарем между дискретной и непрерывной геометрией». Это помогает исследователям переводить экспериментальные результаты в более удобную форму. С помощью этих инструментов исследователи могут лучше исследовать перевернутый с ног на голову мир гиперболического пространства.
Ситуация не совсем похожа на то, как Алиса падает в кроличью нору, но эти эксперименты — возможность исследовать новый мир, в котором удивительные открытия могут скрываться за любым углом, и сам смысл поворота за угол должен быть пересмотрен.
«У этих экспериментов действительно много применений», — сообщил автор новой статьи Игорь Бетчер. «На данный момент невозможно предвидеть, что все можно сделать, но я ожидаю, что у него будет много разнообразных приложений и много крутой физики».
Считается, что в плоском пространстве кратчайшее расстояние между двумя точками — прямая линия, а параллельные линии никогда не пересекаются — независимо от их длины. В искривленном пространстве эти основы геометрии больше не действуют. Математические определения плоского и изогнутого аналогичны повседневному значению в применении к двум измерениям. Вы можете почувствовать основы искривленных пространств, представив (или фактически поиграв) листы бумаги или карты.
Например, поверхность земного шара (или любого шара) является примером двумерного положительно искривленного пространства. А если вы попытаетесь превратить плоскую карту в глобус, то лишняя бумага «сморщится», когда вы изогнете ее в сферу. Чтобы получить гладкую сферу, вы должны потерять лишнее пространство, в результате чего параллельные линии в конечном итоге встретятся, например, линии долготы, которые начинаются параллельно на экваторе, встречающемся на двух полюсах. Из-за этой потери вы можете думать о положительно изогнутом пространстве как о менее просторном пространстве, чем плоское.
Гиперболическое пространство противоположно положительно искривленному пространству — более просторному пространству. Гиперболическое пространство изгибается от самого себя в каждой точке. К сожалению, не существует гиперболического эквивалента шара, в который можно было бы вдавить двумерный лист; он буквально не впишется в то пространство, в котором мы живем.
Лучшее, что вы можете сделать, это сделать форму седла (или форму Прингла), в которой окружающий лист гиперболически изгибается от центральной точки. Сделать каждую точку на листе такой же гиперболической невозможно; нет способа продолжать изгибать и добавлять бумагу, чтобы создать вторую идеальную седловую точку, не сбивая и не искажая первую гиперболическую седловую точку.
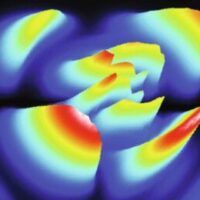
Дополнительное пространство гиперболической геометрии делает ее особенно интересной, поскольку означает, что появляется больше места для образования соединений. Различия в возможных путях между точками влияют на то, как частицы взаимодействуют и какую однородную сетку — например, семиугольную сетку, показанную выше — можно создать. Использование дополнительных соединений, которые возможны в гиперболическом пространстве, может затруднить полное отрезание участков сети друг от друга, что может повлиять на дизайн сетей, таких как Интернет.
Поскольку физически создать гиперболическое пространство на Земле невозможно, исследователи вынуждены довольствоваться лабораторными экспериментами, воспроизводящими некоторые особенности искривленного пространства. Коллар и его коллеги ранее показали, что они могут моделировать однородное двумерное искривленное пространство. Моделирование выполняется с использованием схем, которые служат очень организованным лабиринтом для прохождения микроволн.
Особенностью схем является то, что микроволны безразличны к форме содержащих их резонаторов и зависят только от их общей длины. Также не имеет значения, под каким углом соединяются разные пути. Коллар понял, что эти факты означают, что физическое пространство контура можно эффективно растягивать или сжимать, чтобы создать неевклидово пространство — по крайней мере, в том, что касается микроволн.
В своей предыдущей работе Коллар и его коллеги смогли создать лабиринты с различными формами зигзагообразных путей и продемонстрировать, что схемы моделируют гиперболическое пространство. Несмотря на удобство и упорядоченность используемых схем, физика, проявляющаяся в них, по-прежнему представляет собой странный новый мир, требующий новых математических инструментов для эффективной навигации.
Гиперболические пространства ставят перед физиками несколько иные математические задачи, чем евклидовы пространства, в которых они обычно работают. Например, исследователи не могут использовать стандартный физический трюк, представляющий решетку, становящуюся все меньше и меньше, чтобы выяснить, что происходит с бесконечно маленькой сеткой, которая должна действовать как гладкое непрерывное пространство. Это связано с тем, что в гиперболическом пространстве форма решетки изменяется вместе с ее размером из-за искривления пространства. Новая статья устанавливает математические инструменты, такие как словарь между дискретной и непрерывной геометрией, чтобы обойти эти проблемы и разобраться в результатах моделирования.
С помощью новых инструментов исследователи могут получать точные математические описания и прогнозы, а не просто делать качественные наблюдения. Словарь позволяет им изучать непрерывные гиперболические пространства, даже если моделирование представляет собой только сетку. С помощью словаря исследователи могут взять описание микроволн, перемещающихся между отдельными точками сетки, и преобразовать их в уравнение, описывающее плавную диффузию, или преобразовать математические суммы по всем узлам сетки в интегралы, что более удобно в определенных ситуациях.