Математики открыли девятое число Дедекинда после 32 лет поисков

После трех десятилетий поисков и с некоторой помощью суперкомпьютера математики наконец открыли новый пример специального целого числа, называемого числом Дедекинда.
Только девятое в своем роде, или D (9), он равен 286 386 577 668 298 411 128 469 151 667 598 498 812 366, если вы обновляете свои собственные записи. Этот 42-значный монстр следует за 23-значным числом D(8), открытым в 1991 году.
Нематематикам сложно понять концепцию числа Дедекинда, не говоря уже о том, чтобы разработать его. На самом деле, задействованные вычисления настолько сложны и включают такие огромные числа, что не было уверенности, что D(9) когда-либо будет открыта.
«В течение 32 лет вычисление D(9) было открытая задача, и было сомнительно, что вообще когда-нибудь удастся вычислить это число», — говорит ученый-компьютерщик Леннарт Ван Хиртум из Падерборнского университета в Германии.
В центре Дедекинда число — это логические функции или своего рода логика, которая выбирает выход из входных данных, состоящих всего из двух состояний, таких как истина и ложь или 0 и 1.
Монотонные логические функции — это те которые ограничивают логику таким образом, что замена 0 на 1 во входных данных приводит только к изменению выходных данных с 0 на 1, а не с 1 на 0.
Исследователи описывают он использует красный и белый цвета, а не 1 и 0, но идея та же.
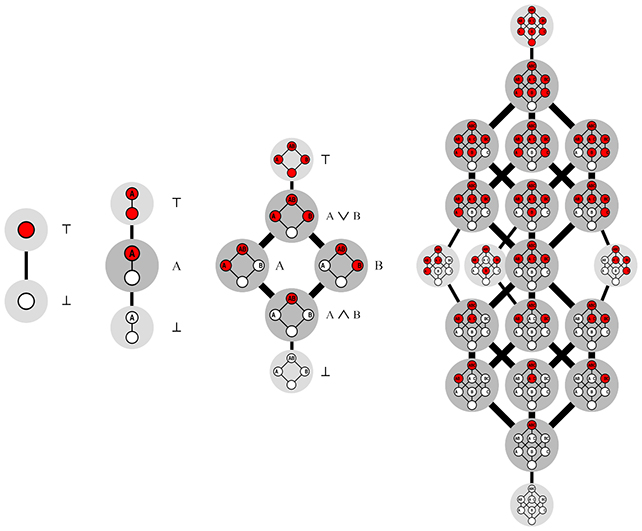
«По сути, вы можете думать о монотонной булевой функции в двух, трех и бесконечных измерениях как об игре с n-мерным кубом», — говорит Ван Хиртум.
«Вы балансируете куб на одном углу, а затем окрашиваете каждый из оставшихся углов либо в белый, либо в красный цвет.»
«Есть только одно правило: вы никогда не должны ставить белый угол над красным. Это создает своего рода вертикальное красно-белое пересечение. Цель игры — посчитать, сколько существует различных разрезов».
Первые несколько довольно прямолинейны. Математики считают D(1) всего за 2, затем 3, 6, 20, 168…
Еще в 1991 году суперкомпьютеру Cray-2 (один из самых мощных суперкомпьютеров того времени) и математику Дугу Видеманну понадобилось 200 часов, чтобы вычислить D(8).
D(9) оказался почти в два раза длиннее D(8) и требовал особого типа суперкомпьютера: такого, который использует специализированные устройства, называемые программируемыми вентильными матрицами (FPGA), которые могут выполнять несколько параллельных вычислений. к суперкомпьютеру Noctua 2 в Падерборнском университете.
«Решение сложных комбинаторных задач с помощью ПЛИС — многообещающая область применения, и Noctua 2 — один из немногих суперкомпьютеров в мире, с которым эксперимент вообще возможен. », — говорит ученый-компьютерщик Кристиан Плессл, глава Падерборнского центра параллельных вычислений (PC2), где хранится Noctua 2.
Потребовалась дальнейшая оптимизация, чтобы дать Noctua 2 возможность работать. Используя симметрию в формуле, чтобы сделать процесс более эффективным, исследователи дали суперкомпьютеру вычислить одну огромную сумму, которая включала 5,5*10^18 членов (количество песчинок на Земле оценивается в 7,5*10^). 18, для сравнения).
Через пять месяцев Noctua 2 дал ответ, и теперь у нас есть D(9). Исследователи пока не ссылались на D(10), но мы можем предположить, что на его поиск может уйти еще 32 года.
Пока нет отчета об исследовании, но она должна быть представлена в сентябре на Международном семинаре по булевым функциям и их приложениям (BFA), который проходит в Норвегии.