Математики нашли девятое число Дедекинда после 32 лет поисков

После трех десятилетий поисков и при некоторой помощи суперкомпьютера математики наконец открыли новый пример специального целого числа, называемого числом Дедекинда.

Только девятое в своем роде, или D (9), оно рассчитывается как 286 386 577 668 298 411 128 469 151 667 598 498 812 366, если вы обновляете свои собственные записи. Этот 42-значный монстр следует за 23-значным D(8), открытым в 1991 году.

Понять концепцию числа Дедекинда сложно нематематикам, не говоря уже о том, чтобы разобраться в ней. Фактически, расчеты настолько сложны и включают в себя такие огромные числа, что не было уверенности в том, что D(9) когда-либо будет открыта.

«В течение 32 лет вычисление D(9) было Это была открытая задача, и было сомнительно, что вообще когда-нибудь можно будет вычислить это число», — сказал ученый-компьютерщик Леннарт Ван Хиртум из Университета Падерборна в Германии еще в июне, когда это число было объявлено.

В центре числа Дедекинда находятся логические функции или своего рода логика, которая выбирает выход из входов, состоящих всего из двух состояний, таких как истина и ложь или 0 и 1.

>

Монотонные логические функции — это те, которые ограничивают логику таким образом, что замена 0 на 1 во входных данных приводит только к изменению выходных данных с 0 на 1, а не с 1 на 0.

Исследователи описывают это, используя красный и белый цвета, а не 1 и 0, но идея та же.

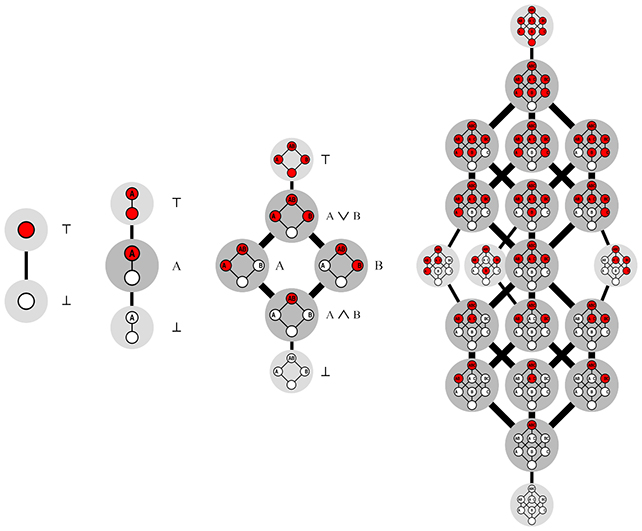
«По сути, вы можете думать о монотонной логической функции в двух, трех и бесконечных измерениях как об игре с n-мерным кубом», — сказал Ван Хиртум.

«Вы балансируете куб по одному углу, а затем окрашиваете каждый из оставшихся углов в белый или красный цвет.»

«Есть только одно правило: вы никогда не должны размещать белый угол выше сделано. Это создает своего рода вертикальное красно-белое пересечение. Цель игры — подсчитать, сколько существует различных разрезов».

Первые несколько довольно просты. Математики считают D(1) всего лишь за 2, затем за 3, 6, 20, 168…

В 1991 году суперкомпьютеру Cray-2 (одному из самых мощных суперкомпьютеров того времени) и математику Дугу Видеманну потребовалось 200 часов, чтобы вычислить D(8).

D(9) оказался почти в два раза длиннее D(8), и потребовался суперкомпьютер особого типа: тот, который использует специализированные блоки, называемые программируемыми вентильными матрицами (FPGA), которые могут выполнять несколько вычислений параллельно. команде суперкомпьютера Noctua 2 в Университете Падерборна.

«Решение сложных комбинаторных задач с помощью FPGA — многообещающая область применения, и Noctua 2 — один из немногих суперкомпьютеров в мире, с помощью которых эксперимент вообще возможен. », — говорит ученый-компьютерщик Кристиан Плессл, глава Падерборнского центра параллельных вычислений (PC2), где хранится Noctua 2.

Чтобы Noctua 2 было с чем работать, потребовались дальнейшие оптимизации. Используя симметрию в формуле, чтобы сделать процесс более эффективным, исследователи дали суперкомпьютеру для вычисления одну огромную сумму, состоящую из 5,5*10^18 членов (количество песчинок на Земле оценивается в 7,5*10^). 18, для сравнения).

Через пять месяцев Noctua 2 нашла ответ, и теперь у нас есть D(9). На данный момент исследователи не упоминали D(10), но мы можем предположить, что на его поиск может уйти еще 32 года.

Работа была представлена ​​в сентябре на Международном семинаре по Булевы функции и их приложения (BFA) в Норвегии.

Предыдущая версия этой статьи была впервые опубликована в июне 2023 года.